Frank R. Schmidt

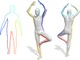
We propose the first algorithm for non-rigid 2D-to-3D shape matching, where the input is a 2D query shape as well as a 3D target shape and the output is a continuous matching curve represented as a closed contour on the 3D shape. We cast the problem as finding the shortest circular path on the product 3-manifold of the two shapes.
We prove that the optimal matching can be computed in polynomial time with a (worst-case) complexity of O(mn²log(n)), where m and n denote the number of vertices on the 2D and the 3D shape respectively. Quantitative evaluation confirms that the method provides excellent results for sketch-based de- formable 3D shape retrieval.

This paper is also stored on arXiv.

@InProceedings\{LRSBC16a,
  author       = "L{\"a}hner, Zorah and Rodol\`a, Emanuele and Schmidt, Frank R. and Bronstein, Michael M. and Cremers, Daniel",
  title        = "Efficient Globally Optimal 2D-to-3D Deformable Shape Matching",
  booktitle    = "IEEE Conference on Computer Vision and Pattern Recognition (CVPR)",
  month        = "Jun",
  year         = "2016",
  url          = "http://frank-r-schmidt.de/Publications/2016/LRSBC16a"
}