Summary

My research interests are in developing efficient and mathematical consistent algorithms that solve Computer Vision problems. In particular I am interested in problems that can be formulated as an energy minimization problem. In the past I worked on shape related problems and on model estimation problems. Depending on the problem, I worked either on discrete or continuous approaches which involved but were not restricted to Differential Geometry, Partial Differential Equations, Convex and Non-Convex Optimization as well as Planar Graphs, Integer Linear Programming and Hierarchical Model Estimation.

Recent Projects

Medical Image Segmentation

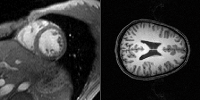Medical image segmentation can be address as a nested multilabeling problem. In our recent work, we showed that incorporating maximal Hausdorff distance constraints provides us with useful image segmentations.

Image Segmentation

The goal of image segmentation is to seperate the image into multiple regions. In our recent work using superlabels, we showed that even binary segmentation can be stated as a multi-label problem with a more accurate result than the classical Boykov-Jolly approach.

3D Shape Matching

Image Segmentation The goal of shape matching is to find a correspondence map between two different shapes. For 3D shapes, there exists no polynomeous runtime methods that solve this problem globally. In our recent work, we showed that by solving an ILP (Integer Linear Program) instance, the 3D shape matching approach can be formulated in a geometrical consistent manner.

2D Shape Matching

Image Segmentation In the case of planar shapes, the matching can be computed quite efficiently, e.g., by different almost quadratic runtime approaches. We presented methods that can do this by either finding multiple shortest paths in a planar grid or by computing a minimal graph cut within a planar graph.

Shape Morphing

The set of all planar shapes can be described as a manifold in an infinite dimensional vector space. By calculating the shortest distance between two shapes (points on the manifold), we receive a transformation from one shape into the other -- a so called morphing. We showed in our work that a path-shortening approach can be much faster the previously used shooting method.