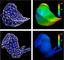
A Combinatorial Solution to Non-Rigid 3D Shape-to-Image Matching
IEEE Conference on Computer Vision and Pattern Recognition (CVPR) - Jul 2017
Download the publication: 5.2 MB
We propose a combinatorial solution for the problem of non-rigidly
matching a 3D shape to 3D image data. To this end, we model the shape
as a triangular mesh and allow each triangle of this mesh to be
rigidly transformed to achieve a suitable matching to the image. By
penalising the distance and the relative rotation between neighbouring
triangles our matching compromises between the image and the shape
information.
In this paper, we resolve two major challenges: Firstly, we address the resulting large and NP- hard combinatorial problem with a suitable graph-theoretic approach. Secondly, we propose an efficient discretisation of the unbounded 6-dimensional Lie group SE(3). To our knowledge this is the first combinatorial formulation for non-rigid 3D shape-to-image matching.
In contrast to existing local (gradient descent) optimisation methods, we obtain solutions that do not require a good initialisation and that are within a bound of the optimal solution. We evaluate the proposed combinatorial method on the two problems of non-rigid 3D shape-to-shape and non-rigid 3D shape-to-image registration and demonstrate that it provides promising results.
This paper is also stored on arXiv.
In this paper, we resolve two major challenges: Firstly, we address the resulting large and NP- hard combinatorial problem with a suitable graph-theoretic approach. Secondly, we propose an efficient discretisation of the unbounded 6-dimensional Lie group SE(3). To our knowledge this is the first combinatorial formulation for non-rigid 3D shape-to-image matching.
In contrast to existing local (gradient descent) optimisation methods, we obtain solutions that do not require a good initialisation and that are within a bound of the optimal solution. We evaluate the proposed combinatorial method on the two problems of non-rigid 3D shape-to-shape and non-rigid 3D shape-to-image registration and demonstrate that it provides promising results.
This paper is also stored on arXiv.
Images and movies
BibTex references
@InProceedings\{BSTC17,
author = "Bernard, Florian and Schmidt, Frank R. and Thunberg, Johan and Cremers, Daniel",
title = "A Combinatorial Solution to Non-Rigid 3D Shape-to-Image Matching",
booktitle = "IEEE Conference on Computer Vision and Pattern Recognition (CVPR)",
month = "Jul",
year = "2017",
url = "http://frank-r-schmidt.de/Publications/2017/BSTC17"
}