Frank R. Schmidt

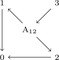
Solving a multi-labeling problem with a convex penalty can be achieved in polynomial time if the label set is totally ordered. In this paper we propose a generalization to partially ordered sets. To this end, we assume that the label set is the Cartesian product of totally ordered sets and the convex prior is separable. For this setting we introduce a general combinatorial optimization framework that provides an approximate solution. More specifically, we first construct a graph whose minimal cut provides a lower bound to our energy. The result of this relaxation is then used to get a feasible solution via classical move-making cuts. To speed up the optimization, we propose an efficient coarse-to-fine approach over the label space. We demonstrate the proposed framework through extensive experiments for optical flow estimation.

@InProceedings\{DSC18,
  author       = "Domokos, Csaba and Schmidt, Frank R. and Cremers, Daniel",
  title        = "MRF Optimization with Separable Convex Prior on Partially Ordered Labels",
  booktitle    = "European Conference on Computer Vision (ECCV)",
  month        = "Sep",
  year         = "2018",
  url          = "http://frank-r-schmidt.de/Publications/2018/DSC18"
}